Das Lambdoma

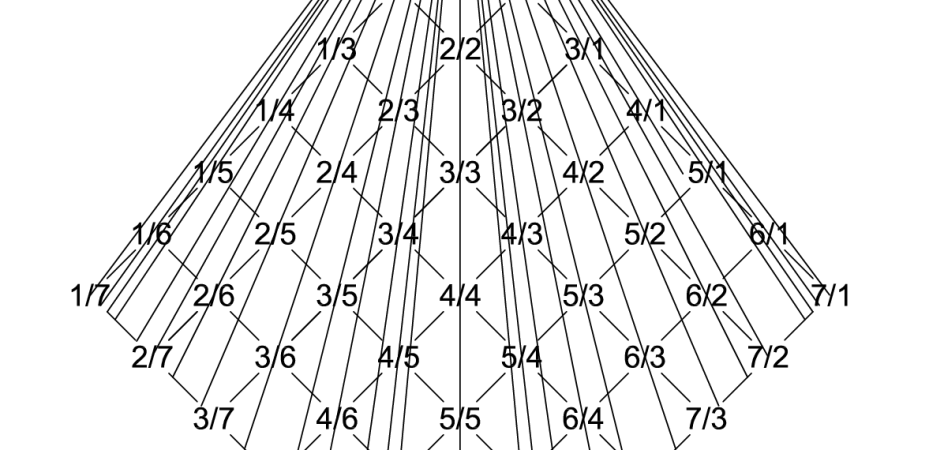
Wenn wir Töne hören, so macht der einzelne Ton alleine noch keinen nennenswerten Eindruck auf unser Gemüt. Die Empfindung entsteht, wenn zwei Töne aufeinanderfolgen, oder gleichzeitig erklingen und beide stehen in einem rationalen Verhältnis mit kleinen Zahlen. Man spricht von einem Intervall, wenn etwa das mittlere C mit einer Frequenz von 264 Hz, gefolgt vom C‘ der nächsten Oktave mit 528 Hz erklingt. Die Tonfolge besitzt das Frequenzverhältnis 1:2 oder 1/2 (gesprochen eins zu zwo). Oder, wenn etwa die Tonfolge C – G erklingt, so steht auch diese Tonfolge in einem einfachen Frequenzverhältnis 264 Hz : 396 Hz = 2:3 = 2/3. Alle diese Tonfolgen bilden Frequenzverhältnisse und können in geordneter Form dargestellt werden, siehe Abbildung links.

Das Zahlenschema nennt man in der Harmonik Lambdoma, weil es die Form des griechischen Buchstaben Lambda besitzt. Das Netz von Geraden, die sich von oben nach unten erstrecken, nennt man Gleichtonlinien. Sie laufen durch Brüche gleicher Werte, wie etwa 1/2 = 2/4 = 4/8 …

Die Zahlen 1/2, 2/3, … nennt man rationale Zahlen. Sie sind im Lambdoma in Bruchschreibweise dargestellt. Vergrößert man das Lambdoma nach unten, so können damit alle rationalen Zahlen dargestellt werden.

Die „Zeugertonlinie“ läuft durch die Brüche 1/1, 2/2, 3/3, …, steht für den Grundton eines Intervalls und teilt das Lambdoma in der Mitte. Auf der einen Seite stehen dann alle Intervalle größer als 1, auf der anderen kleiner als 1. So etwa steht die Dominante mit der Frequenz 3/2 auf einer, die Subdominante mit der Frequenz 2/3 auf der anderen Seite.

In Hans Kaysers Lehrbuch der Harmonik ist das Lambdoma neben einem Monochord platziert. So kann man den Zusammenhang zwischen Intervall und Zahlenproportion (rationale Zahl) sehen.

Neben den Bruchzahlen sind jeweils die Tonbezeichnungen angegeben. Ich habe mit zunächst für eigene Zwecke ein Klanglambdoma programmiert. Darauf werden durch Überfahren mit dem Mauszeiger die von Hans Kayser angegebenen Tonbezeichnungen, die Stegposition und die Frequenz eingeblendet. Die Intervalle sind per Mausklick einzeln (nicht als Intervall) hörbar. Es gibt viele weitere Funktionen. Gegen eine Gebühr von 100 € vertreibe ich die Software. (Mail im Impressum)

Durch Einblenden der Gleichtonlinien wird ihre fraktale Struktur deutlich.

Einblick in das Lehrbuch der Harmonik von Hans Kayser. Er nennt das Lambdoma auch Teiltondiagramm.

Zweierlei Wesen von Zahl

Wir stellen fest, dass die rationalen Zahlen, als Bruchzahlen dargestellt auf zweierlei Weise gedeutet werden. Zum einen sind sie Bruchzahlen zum Andern Intervallverhältnisse. Dies bedarf einer genaueren Erklärung -> Eine philosophische Betrachtung über das Intervallepfinden

Wir sehen also, dass Intervalle zwar vermittels der Physik von Tönen und Klängen transportiert werden. Dass aber das Intervallempfinden auf dem reinen Zahlenverhältnis (rationalen Zahl) beruht. Zahl an und für sich gesehen ist nach Kant Voraussetzung für das Zeitempfinden und für Kausalität. Erst der zählende Mensch besitzt das Wissen von einem vorher und einem nachher. Er weiß, dass den Ereignissen Ereignisse vorausgehen, und schließt daraus auf Kausalität.

Zahl ist also ein ganz zentrales Element menschlicher Existenz und menschlichem Bewusstseins. Zahlproportion kann daher mit Fug und Recht als Intervall angesehen werden. Diese Interpretation ist der Zahl so nahe, dass sie als sekundäre Interpretation von Zahl ein der Zahl an sich naheliegendes Wesen besitzt.

Darin liegt auch der tiefere Grund und die Berechtigung mit der Harmoniker in jeglichen Zahlenproportionen Intervalle sehen. Genauer gesagt, kann das Wesen von Intervallen und Zahlen nicht getrennt werden, denn Zahl liegt im Wesen des Menschen verborgen und das Intervall als die Fähigkeit Musik zu hören ist damit wesenhaft verknüpft.

In seinem Brief vom 27. April 1712 an Christian Goldbach äußert Gottfried Wilhelm Leibniz den berühmten Gedanken „Musica est exercitium arithmeticae occultum nescientis se numerare animi.“ – „Musik ist die verborgene Mathematik der unbewusst rechnenden Seele.“

Das Lambdoma als Darstellung aller rationalen Zahlen ist daher von großer Bedeutung für die Harmonik.

Als Zahlenmatrix sind Zähler und Nenner der Bruchzahlen im Lambdoma eine schlichte aufsteigende Reihe von ganzen Zahlen. Die Matrix kombiniert jeden Nenner mit jedem Zähler und so werden alle Bruchzahlen erfasst.

Das Lambdoma ist sehr alt

Albert von Thimus (1806-1878) entdeckte ein bis dahin unverstandenes Zitat in einem Kommentar von Jamblichos (neuplatonischer Philosoph 3. Jh. n. Chr.) zur kleineren Arithmetik des Nikomachos (neuplatonischer Philosoph 2. Jh. n. Chr). Dort heißt es :

„Von der Einheit aus wird von einem Winkel aus eine Figur in Gestalt des Lambda gezeichnet. Auf der einen Seite der Reihe werden die an die Einheit sich anschließenden Zahlen aufgezeichnet. Die andere Seite wird – beginnend von dem größten der Teile, welcher das seiner Größe nach dem Ganzen zunächst liegende Halbe ist – der Reihe nach mit den hieran sich anschließenden Teilen beschrieben.“

Diese Hinweise, wie auch das Originalzitat ist in Hans Kayers Lehrbuch der Harmonik zu finden.
(Kayser, Hans; Lehrbuch der Harmonik; Zürich, Occident, 1950, S. 60)

Das Zitat bei A. v. Thimus in seinem zweibändigen Werk Die harmonikale Symbolik des Alterthums, nachzulesen. Thimus versuchte nachzuweisen dass die Harmonik und das Lambdoma bereits im Altertum bekannt und fester Bestandteil der Mysterien waren.
Online Literatur zur Harmonik

Siehe auch Die Geschichte der pythagoreischen Harmonik, ein kurzer Überblick.

Die Wiederentdeckung des Lambdoma durch Georg Cantor (1845 – 1918)

Cantor bewies mittels des „Diagonalverfahrens“ (erstes Diagonalargument), dass die Menge der rationalen Zahlen (Bruchzahlen) abzählbar und unendlich und die Menge der reellen Zahlen überabzählbar ist (zweites Diagonalargument).
Was Cantor gemacht hat. Er hat das als Lambdoma bekannte Zahlenschema auf eine Ecke gestellt, um es so mäandernd abzählen zu können. Cantor wusste nicht, dass das Lambdoma seit zweitausend Jahren schon bekannt war.